I'm late publishing the newsletter this week. Summer got the better of me, and I was relaxing around a campfire with friends and family last night. Don't tell Wartull though. He gets a little irregular when the devs have a social life.
Let's dive in. This week's Dev's Journal will cover using the new Forge Coverage tool to improve test coverage and how to think about approximating real-valued equations (i.e. defined on the Real Number line) with integer arithmetic in Solidity.
Build: Improving Test Coverage with Forge
As we're remediating audit findings and doing clean-up on the Olympus Bophades system, one area we've been looking at is ensuring our test coverage is high across the codebase. In layman's terms, this means we're trying to make sure we have tests written that cover all the possible routes through the code to ensure it behaves correctly.
There are multiple tools available for this, such as the solidity-coverage plugin for Hardhat, and DappTools coverage, but Foundry recently released the first version of Forge Coverage so I decided to give that a spin (disclaimer: early stage software).
The basic command forge coverage analyzes all files in your repo (outside of the lib folder) and then runs your tests suite (all files with .t.sol) to provide a console printed report with the percent of lines of code hit, branches hit, and functions hit by the tests.
Forge coverage can also provide a coverage report file by doing forge coverage —report lcov. Then, you can use a VS Code extension like Coverage Gutters to display which lines in a file aren’t hit by the tests. To run the extension, simply open the file you would like to see coverage for and run Coverage Gutters: Display Coverage from the command palette (accessible with Cmd+Shift+P on a Mac). Each line will be highlighted with a small indicator on the left hand side of the editor with the status. Green means that the line is covered. Yellow means that the line is covered, but not all branches (happens on an if statement or other branching logic). Red means the line is not covered.
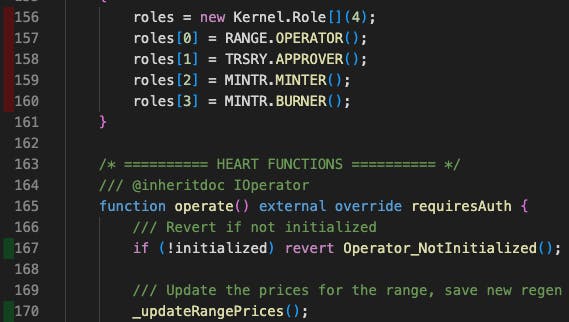
It’s not perfect, but it’s helping me fill some gaps. I had to revert my foundry version to a nightly build from last week since the recently merged "better branching" version fails on our repository (see this GitHub issue). That being said, the older version I'm using doesn't recognize some test files so the coverage of certain contracts seems really low. For example, there is a test file that 100% covers the PRICE.sol contract referenced below, but it is only recognizing the lines of code hit by other test suites in this report.

Overall, forge coverage is still an early release tool, but I can see it quickly becoming an integral part of my testing stack. The team has prioritized the development of this feature and others in the community are helping to improve it. Here is the roadmap for new features and improvements.
Think: Approximating Real-Valued Math with Integers in Solidity
Many smart contract systems, especially in DeFi, use mathematical concepts such as interest calculations, invariants (such as x * y = k), etc. as the basis of their logic. These equations are typically defined on the set of real numbers (in some dimension based on the number of inputs). However, Solidity does not support floating point or fixed point numbers (yet), and, therefore, implementations targeting the EVM must approximate these real-valued systems using integer values and arithmetic. Many will be familiar with the basics of this concept, but they might not appreciate the depth of complexity that this introduces.
Level 1: Multiply then Divide
Anyone who has written a contract that deals with the transfer of value has likely encountered the "decimal" concept used by Ether and ERC20 tokens to denote that integer values representing amounts of tokens should be interpreted as having a certain number of decimal places. The most common is 18 decimals, which is used by Ether, but others exist, typically in the range of 6 to 24 decimals. Solidity variables are at most 256-bits, so an unsigned integer can represent a max value of ~1.157 x 10^77. Therefore, using 18 as a decimal value provides a nice tradeoff between precision (with a large number of decimal places) and enough room for various whole number values and intermediate values during computation. This practice has become the default way to approximate real numbers.
However, we cannot assume "this variable has 18 decimals" and expect everything to magically work. Since these numbers are still in fact integers, they behave like them in multiplication and division operations. For example, assume we have a multiplier 1.25 stored as 1_250 with 3 assumed decimals. Then, if we multiply an 18-decimal token balance of 10 (10_000000000000000000) by the multiplier we get 12,500 tokens (12500_000000000000000000)! Obviously, that's a bit more of an increase than 25%. In order to keep our decimal values consistent, we must apply a scaling factor after multiplication and before division of a number with an assumed decimal value.
For a somewhat practical example, let's assume we have an 18-decimal token and a 6-decimal interest rate percent (which would actually need 8 decimals since percents are less than 1) on a savings contract. The contract stores a user's deposit balance and a total compound factor from the interest that's been applied. Balances are calculated using the difference between the current compound factor and the compound factor at the time of a deposit (similar to many staking contracts).
contract Savings {
ERC20 public token; // token with 18 decimals
uint256 public interestRate; // annual interest rate percent with 6 decimals, e.g. 5125000 = 5.125% = 0.05125
mapping(address => uint256) public depositBalance; // amount of tokens deposited by the user
mapping(address => uint256) public depositCompoundFactor; // compound factor when the user deposited their tokens
uint256 public compoundFactor; // compound factor with 8 decimals, e.g. 125000000 = 1.25
uint256 public lastCompound; // timestamp when the savings contract was last compound
uint256 public compoundFrequency; // how often to compound the interest earned.
function compoundInterest() public {
require(block.timestamp >= lastCompound + compoundFrequency, "Cannot compound yet");
compoundFactor = (compoundFactor * (1e8 + interestRate / (365 days / compoundFrequency))) / 1e8;
lastCompound = block.timestamp;
}
function getBalance(address user) {
uint256 compoundToApply = (compoundFactor * 1e8) / depositCompoundFactor[user];
uint256 balance = (depositedBalance[user] * compoundToApply) / 1e8;
return balance;
}
}
In the getBalance function, we have to divide the current compoundFactor by the one when the user deposited to get the amount of compound interest to apply to their balance. In order to do so, we first scale the compoundFactor by 8 decimals (1e8) and then divide by depositedCompoundFactor[user]. Let's break this down in the order of operations using example values:
(1_50000000 * 1_00000000) = 150000000_00000000150000000_00000000 / 1_20000000 = 1_25000000
Consider if the parentheses were changed so that the division is done first:
(1_00000000 / 1_20000000) = 01_50000000 * 0 = 0
The calculation breaks because the first operation results in a fractional value, which is rounded down to zero by integer floor division.
On the next line, we need to multiply their initial balance by this calculated factor, so we do then multiplication first and scale the amount down. Using example values, the order of operations is then:
(1000_000000000000000000 * 1_25000000) = 125000000000_000000000000000000125000000000_000000000000000000 / 1_00000000 = 1250_000000000000000000
Consider if the parentheses were changed so that the division is done first:
(1_25000000 / 1_00000000) = 11000_000000000000000000 * 1 = 1000_000000000000000000
The results aren't as catastrophic as the first example, but the user does not earn any interest since the compound factor lost all precision in the first operation due to integer division rounding.
Multiplication and division have equal precedence in Solidity, so if a multiplication is listed first, it will be performed before the division without the need for parentheses; however, parentheses are used to make this explicit in the example.
There are some math libraries that provide custom types with certain decimal sizes and have functions that handle scaling as a convenience wrapper, such as PRBMath. Additionally, some implement approximations for certain math operations like sqrt and log, which may be useful.
Level 2: Phantom Overflows
While understanding the basic "multiply then divide" framework will get you pretty far, it is not completely sufficient. Another potential issue to consider is overflow errors when multiplying two numbers with large decimal values, i.e. 1e40 * 1e40 = 1e80 -> reverts with an overflow error. While this is fairly uncommon by itself, it can happen in the intermediate step of a "multiply then divide" operation. For example, 1000000e18 * 1_25e53 / 1_00e53 would have 1000000e18 * 1_25e53 = 125e77 as an intermediate result and would overflow even though the final result is 1250000e18. Overflows in the middle of a computation are called "phantom" overflows since the result by itself would still be in bounds.
An obvious way to handle this is to use a larger size variable for the intermediate calculation and then casting back down for the final result, but this assumes you aren't using the maximum variable size already (uint256).
uint128 startBalance = 1000000e18;
uint128 multiplier = 125e20;
uint128 scale = 100e20;
uint128 newBalance = uint128(uint256(startBalance) * uint256(multiplier) / uint256(scale));
// newBalance = 1250000e18
Without casting, this will phantom overflow since the intermediate value 125e44 is greater than the max value for uint128 (~3e38). However, since that is a valid uint256 value, our calculation can succeed. The end result 1250000e18 fits within the range of a uint128 and can be cast back down.
So, how can we do something similar for uint256? One answer is to use two storage slots to represent an intermediate value as a 512-bit variable. Remco Bloemen developed this method which implements phantom overflow protection for the multiply and then divide operation for uint256 values using the Solidity mulmod operation and some assembly wizardy. I colloquially refer to this as the mulDiv operation and have used an implementation of it, which includes a rounding up variant, in the new Olympus Bonds V3 / Permissionless OP contracts.
Level 3: Rounding Errors
So you've handled scaling and phantom overflows, should be good right? Well, there's one more stealthier issue that I've run into: rounding errors. While tiny balance errors in the 18th decimal place of a token that isn't very valuable may be imperceptible in most cases, when dealing with the exchange of value there are cases where this could be a big deal. As discussed in a previous article, Uniswap was especially concerned with this given the permissionless nature of the protocol where it's unknown the future decimal places and value per unit of tokens that will be for any given pool. As an example, let's assume that at a certain exchange rate a user could add liquidity and remove liquidity from a pool and receive 1 wei more of their balance each time. Gas fees may make it so this doesn't make sense for an 18 decimal token that's only worth ~$1000 (therefore, the fractional amount is worth 10^-15 cents). However, imagine a 6-decimal token that is worth $100,000 on a sharded L2 where gas fees are <$0.01 for the transactions, then you'd make ~$1 every time you did the round trip and could drain funds from the pool. This may sound extreme, but a similar exploit happened on Solana late last year due to improperly handled rounding errors.
As a practical matter, there should be a desired behavior for any calculation when approximating a real value with integer arithmetic. In the Bonds V3 system, we want to ensure that payout values are rounded down when calculated so that a final transaction on a market won't cause the capacity to underflow when an allowed amount is specified. To do so, we also have a mulDivUp operation in the math library we're using which takes a ceiling value on division instead of the floor value we see with normal integer division.
To demonstrate, consider the following real-valued price equation from the Bonds V3 system: $$ \Phi(t) = max(\Phi_{min}, D(t) \times \Gamma(t)) $$
where \(\Phi(t)\) is the price of the market, \(D(t)\) is the debt of the market, and \(\Gamma(t)\) is the control variable at time \(t\). and \(\Phi_{min}\) is the minimum price set for the market.
We have to implement this using integer arithmetic and so have to make some decisions about rounding. In this case, we'll say the price will be rounded down using floor division. In order to avoid overflow issues, we use a scale factor \(S\) in the market to convert between the price, debt, and control variable values. We can then write this as: $$ \Phi^{'}(t) = max\left(\Phi_{min}, \left \lfloor \frac{D^{'}(t) \times \Gamma^{'}(t)}{S} \right\rfloor \right) $$
Let's now consider the calculation for a new control variable. During a tune, the new control variable will be calculated from the previous price and a calculated target debt \(\delta(t)\) based on whether the market is over- or undersold at that point in time. I'm not going to provide a full treatment of this here, but consider this equation as an example for our rounding discussion:
$$\Gamma_{*}(t) = max\left(\Gamma(t), \frac{\Phi(t)}{\delta(t)}\right)$$
where \(\Gamma(t)\) is the current control variable, \(\Phi(t)\) is the current price, and \(\delta(t)\) is the target debt calculated at time \(t\).
Note that the control variable can decrease, but that is done is a separate adjustment calculation and applied over an interval. This isn't germane to the current analysis, but may confuse some readers.
In our approximation then, we want the control variable to be rounded up when calculated to preserves the duality of the price equation.
$$ \Gamma_{*}^{'}(t) = max\left(\Gamma^{'}(t), \left\lceil\frac{\Phi^{'}(t) \times S}{\delta^{'}(t)}\right\rceil \right) $$
Once we've determined the desired behaviors for our approximations, we can implement the floor operations using mulDiv and the ceiling operations using mulDivUp.
price = controlVariable.mulDiv(debt, scale)controlVariable = price.mulDivUp(scale, debt)
Here's an example with feasible values:
// Assume we initialize a market with these values
initialPrice = 2e36;
scale = 1e36;
debt = 300000 * 1e18; // = 3e23
// Initial control variable is then
controlVariable = initialPrice.mulDivUp(scale, debt);
// Calculation steps
// initialPrice * scale = 2e36 * 1e36 = 2e72
// 2e72 / debt = 2e72 / 3e23 = 6666666666666666666666666666666666666666666666667 (6.666.. * 1e48)
// The key is that the above value rounded to a 7.
// Then if someone checks the market price, it is calculated as:
price = controlVariable.mulDiv(debt, scale);
// Calculation steps
// controlVariable * scale = 6666666666666666666666666666666666666666666666667 * 3e23 = 2e72
// 2e72 / scale = 2e72 / 1e36 = 2e36
// Consider if the control variable is rounded down as well
controlVariable = initialPrice.mulDiv(scale, debt);
// Calculation steps
// initialPrice * scale = 2e36 * 1e36 = 2e72
// 2e72 / debt = 2e72 / 3e23 = 6666666666666666666666666666666666666666666666666 (6.666.. * 1e48)
// Here, the control variable rounds down to a 6.
// Then the price calculation would be:
price = controlVariable.mulDiv(debt, scale);
// Calculation steps
// controlVariable * scale = 6666666666666666666666666666666666666666666666666 * 3e23 = 1999999999999999999999999999999999999999999999999999999999999999999999999 (1.999... * 1e72)
// 1.999..e72 / scale = 1.999..e72 / 1e36 = 1.999..e36
// Therefore, price =/= initialPrice using the same values.
That's probably enough minutia for one sitting. If you made it this far, congrats on hanging in there and learning more than you probably cared to know about integer arithmetic. In the paper I'm currently writing on a formal treatment of the Bonds V3 system, I model the system as hinted at above and analyze the rounding behaviors of the Olympus implementation.
Currently Reading
Cryptonomicon - Neal Stephenson (Audiobook). I'm still working my way through this on audiobook and it's been a lot of fun. The level of computer science/math nerding out is interesting, but there are a lot of human situations that a lot of people have likely found themselves thinking, but that they've never verbalized. Neal is very insightful and aware of the human condition.


